Aberrations Cheat Sheet
-
This is a list of useful formulas, diagrams, and plots used in first- and third-order aberrations of rotational symmetric optical systems.
The sign convention follows the one adopted by the College of Optical Sciences at the University of Arizona. For a more complete list and guide please refer to “Field Guide to Geometrical Optics” by J.E. Greivenkamp.
-
The transverse ray aberrations are related to the derivative of the wavefront error:
\[\epsilon_y = - \frac{R}{r_p} \frac{ \partial W \left( x_p, y_p \right)}{ \partial y_p }\] \[\epsilon_x = - \frac{R}{r_p} \frac{ \partial W \left( x_p, y_p \right)}{ \partial x_p }\] \[\frac{R}{r_p} = \frac{-1}{n' u' } \approx 2 \, f \#_{W}\]subject to
\[n_2 < n_1\] -
Wavefront expansion:
| $$ W = $$ | $$ W_{020} \rho^2 $$ | Defocus |
| $$ + W_{111} H \rho \cos \theta $$ | Wavefront tilt | |
| Third-Order Terms | ||
| $$ + W_{040} \rho^4 $$ | Spherical | |
| $$ + W_{131} H \rho^3 \cos \theta $$ | Coma | |
| $$ + W_{222} H^2 \rho^2 \cos^2 \theta $$ | Astigmatism | |
| $$ + W_{220} H^2 \rho^2 $$ | Field Curvature | |
| $$ + W_{311} H^3 \rho \cos \theta $$ | Distortion | |
| $$+$$ Fifth-Order Terms | ||
- The meaning of \(W_{IJK}\):
\(W_{IJK}\) is the amount of wavefront error associated with the aberration term at the edge of the pupil \(\left( y_p = 1 \right)\) and the edge of the field \(\left( H = 1 \right)\)
Spherical Aberration:
-
Spherical aberration is a variation of focal length with pupil radius. In other words. Rays that cross the pupil closer to the optical axis will be close to the paraxial focal length but rays at the edge of the pupil will have a different effective focal length.
-
Spherical is an on-axis aberration. It has no dependance on the field \(H\)
\[W = W_{040} \rho^4 = W_{040} \left( x^2_p + y^2_p \right)\] \[\epsilon_y = -4 \frac{R}{r_p} W_{040} \rho^3 \cos \theta\] \[\epsilon_x = -4 \frac{R}{r_p} W_{040} \rho^3 \sin \theta\]Ray fans:
\[\epsilon_y = -4 \frac{R}{r_p} W_{040} y_p^3\] \[\epsilon_x = -4 \frac{R}{r_p} W_{040} x_p^3\]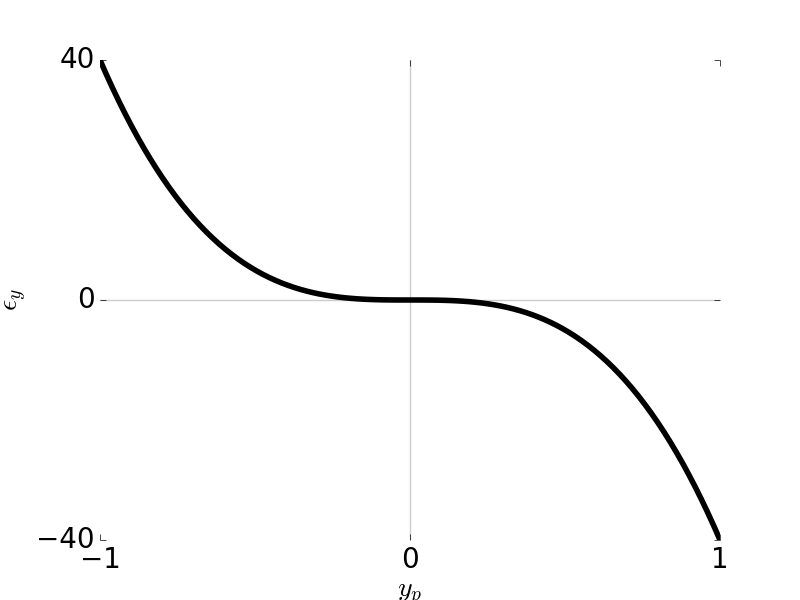
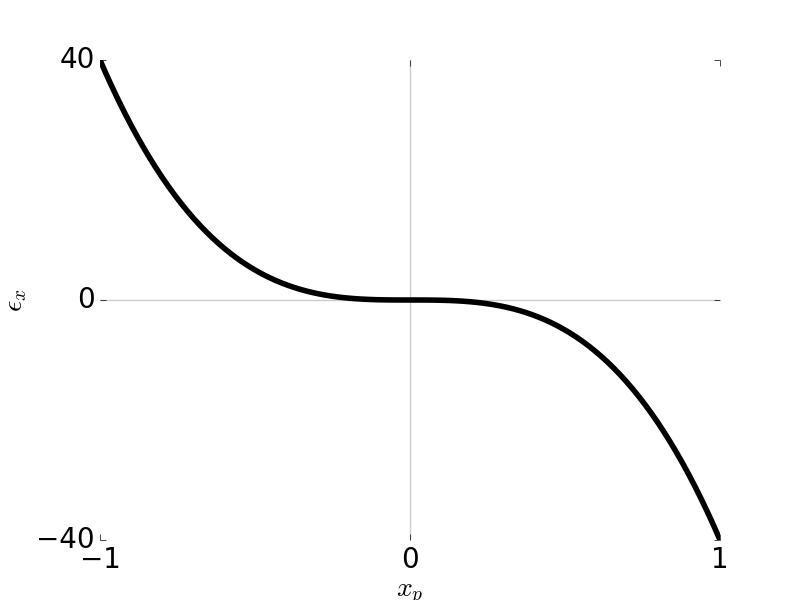 Tangential Ray and Sagittal Ray Fans: Spherical Aberration \(W_{040} = 1\) and \( F / \# \) = 5
Tangential Ray and Sagittal Ray Fans: Spherical Aberration \(W_{040} = 1\) and \( F / \# \) = 5
Coma:
-
Coma is variation in magnification with pupil radius.
-
Coma is an off-axis aberation: the image blur increases linearly proportional to \(H\)
-
For a given object point, each radial zone in the pupil maps to a displaces circle of light in the image blur
-
If \(W_{131} > 0\) the pattern flares toward the optical axis. If \(W_{131} < 0\) the pattern flares away from the optical axis.
\[W = W_{131} H \rho^3 \cos \theta\] \[\epsilon_y = - \frac{R}{r_p} W_{131} H \rho^2 \left( 2 + cos 2 \theta \right)\] \[\epsilon_x = - \frac{R}{r_p} W_{131} H \rho^2 \sin 2 \theta\]Ray fans:
\[\epsilon_y = -3 \frac{R}{r_p} W_{131} y_p^2\] \[\epsilon_x = 0\]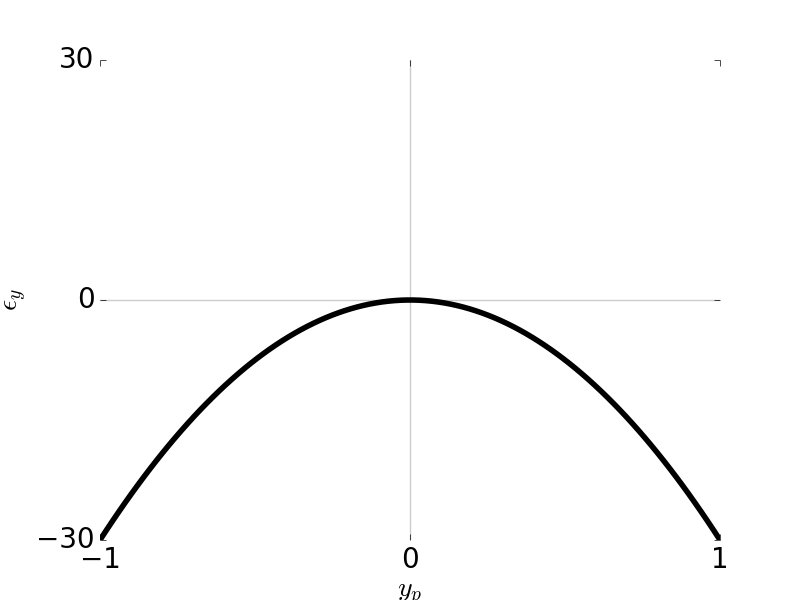
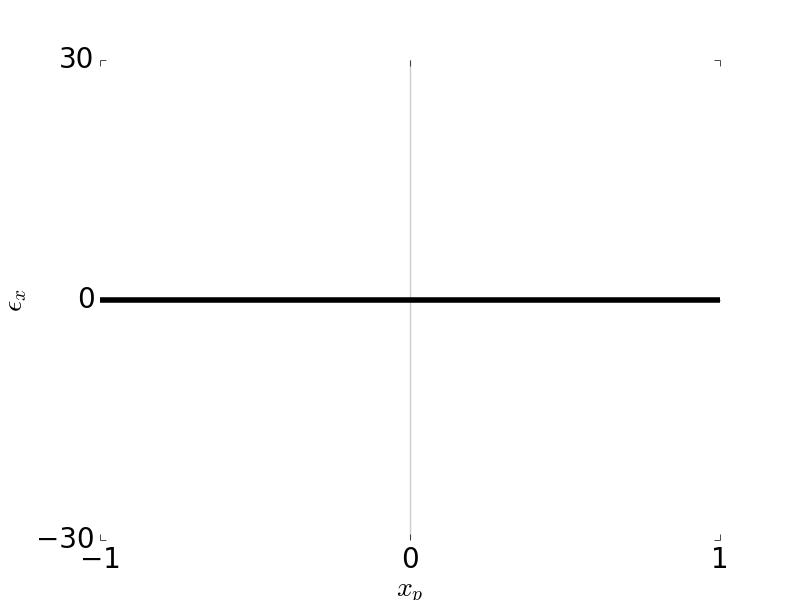 Tangential Ray and Sagittal Ray Fans: Coma \(W_{131} = 1\), \( H \) = 1, \( F / \# \) = 5
Tangential Ray and Sagittal Ray Fans: Coma \(W_{131} = 1\), \( H \) = 1, \( F / \# \) = 5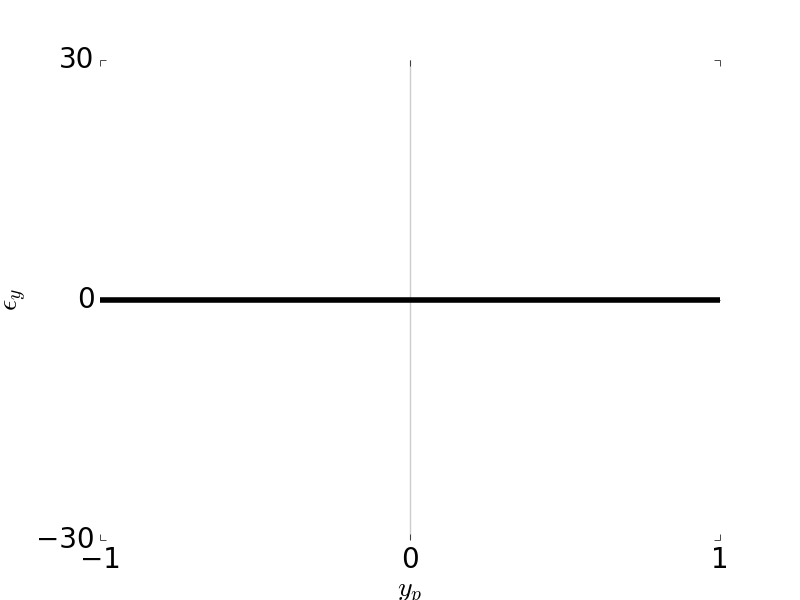
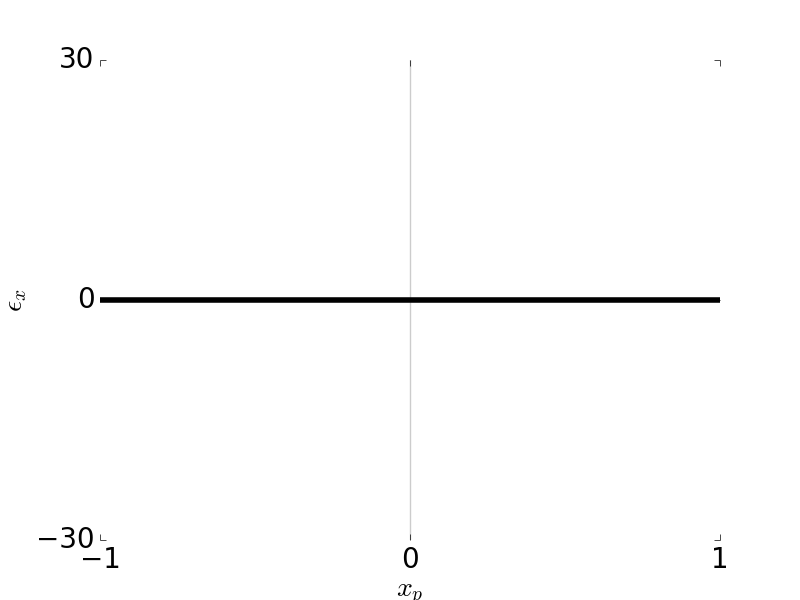 Tangential Ray and Sagittal Ray Fans: Coma \(W_{131} = 1\), \( H \) = 0, \( F / \# \) = 5
Tangential Ray and Sagittal Ray Fans: Coma \(W_{131} = 1\), \( H \) = 0, \( F / \# \) = 5
Astigmatism:
-
The focal length in the horizontal and vertical meridians are different as a function of image height.
-
With positive astigmatism, light from the vertical meridian has a shorter focal length than the horizontal meridian.
-
An object point produces two perpensicular line images, the tangential focus and the sagittal focus.
-
The medial focus is a circular focus located between the tangential and sagittal focus.
-
Astigmatism is an off-axis aberration which depends on the field \(H\) squared. Therefore astigmatism doesn’t occur on axis.
\[W = W_{222} H^2 \rho^2 \cos^2 \theta = W_{222} H^2 y^2_p\]Ray fans:
\[\epsilon_y = -2 \frac{R}{r_p} W_{222} H^2 y_p\] \[\epsilon_x = 0\]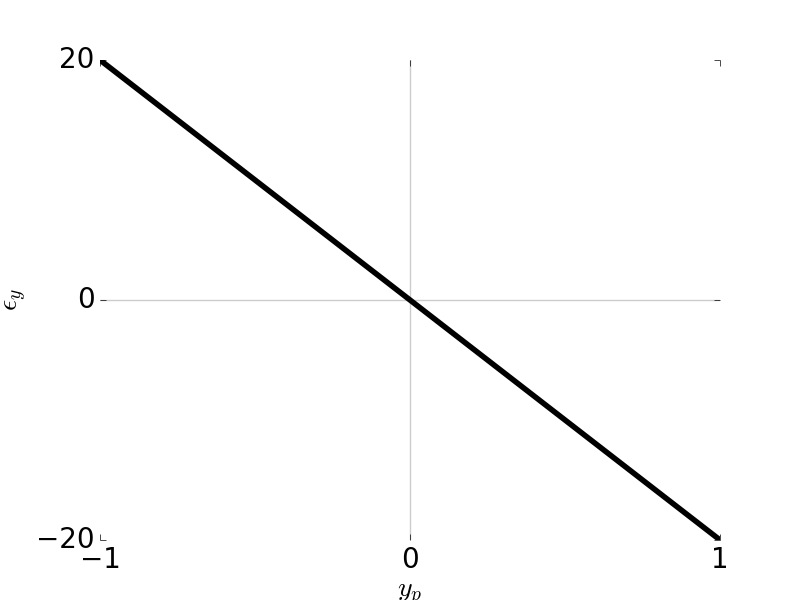
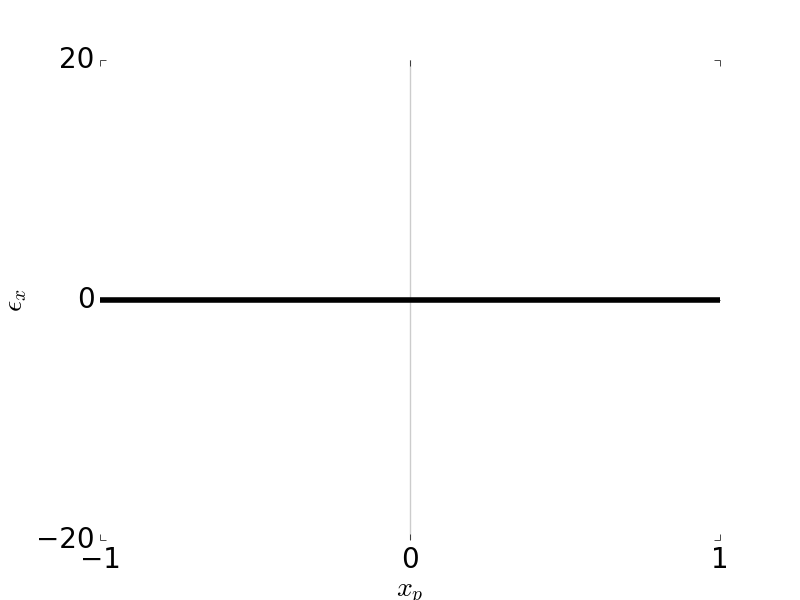 Tangential Ray and Sagittal Ray Fans: Astigmatism \(W_{222} = 1\), \( H \) = 1, \( F / \# \) = 5
Tangential Ray and Sagittal Ray Fans: Astigmatism \(W_{222} = 1\), \( H \) = 1, \( F / \# \) = 5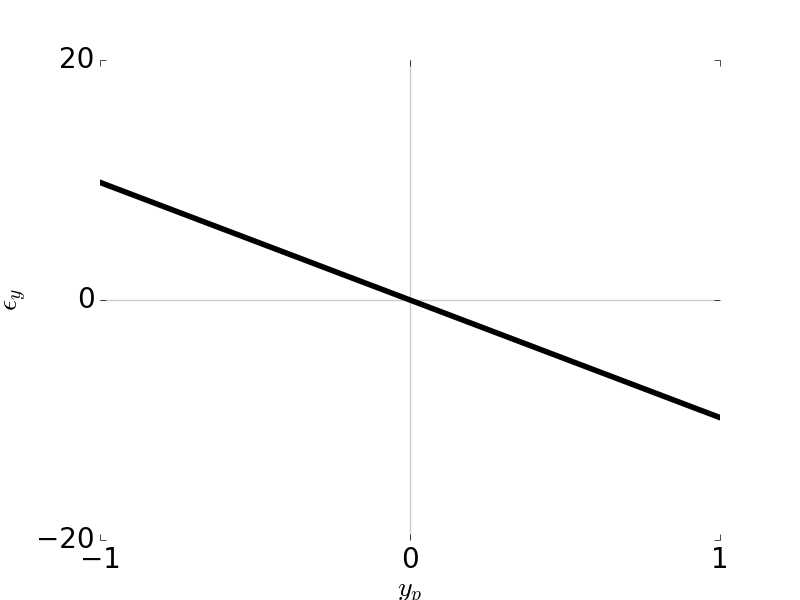
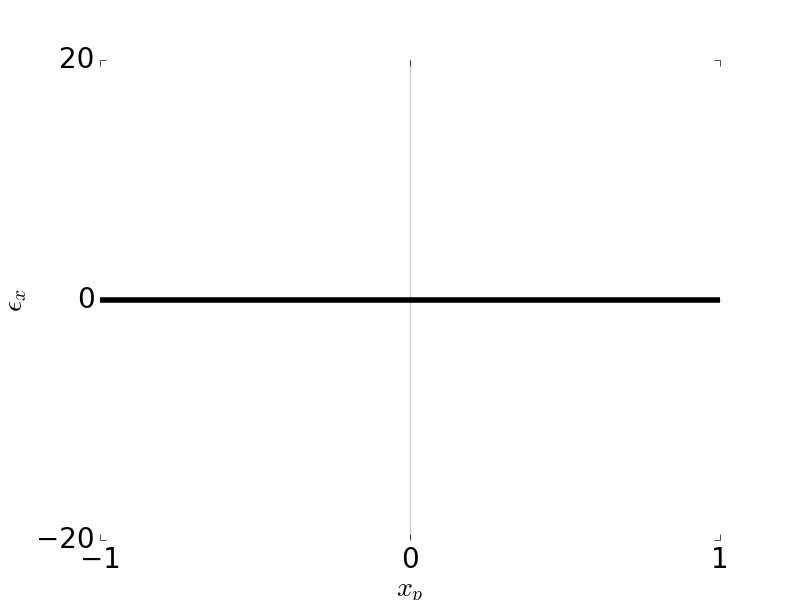 Tangential Ray and Sagittal Ray Fans: Astigmatism \(W_{222} = 1\), \( H \) = 0.7, \( F / \# \) = 5
Tangential Ray and Sagittal Ray Fans: Astigmatism \(W_{222} = 1\), \( H \) = 0.7, \( F / \# \) = 5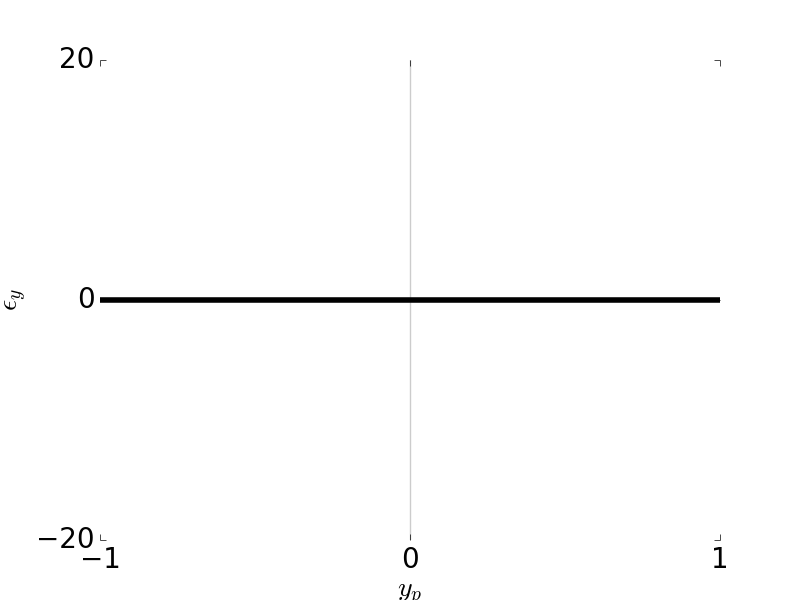
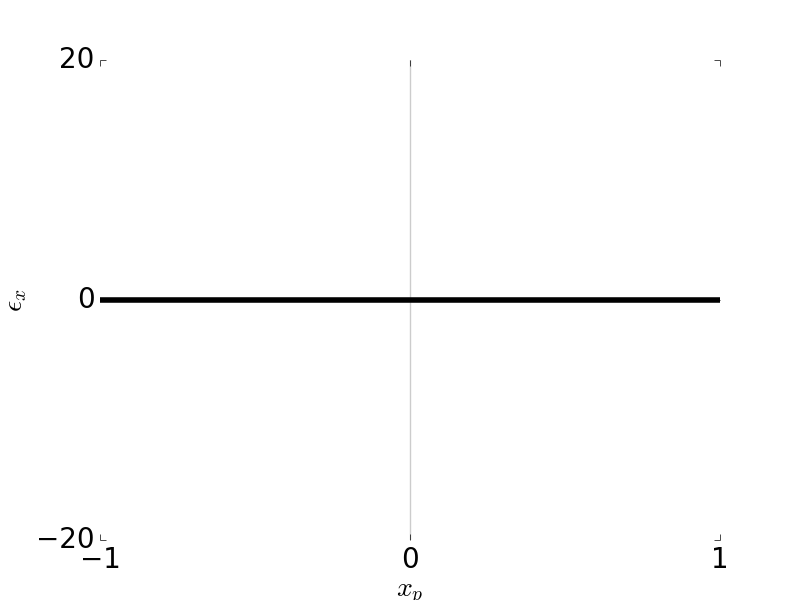 Tangential Ray and Sagittal Ray Fans: Astigmatism \(W_{222} = 1\), \( H \) = 0, \( F / \# \) = 5
Tangential Ray and Sagittal Ray Fans: Astigmatism \(W_{222} = 1\), \( H \) = 0, \( F / \# \) = 5
Field Curvature:
-
The image plane is curved instead of flat.
-
Optical systems have a natural tendency to create curved image planes.
-
In a system with only Field Curvature aberration, a perfect image is formed on a curved surface.
-
A positive singlet has an inward bending image surface.
\[W = W_{220} H^2 \rho^2 = W_{220} H^2 \left( x_p^2 + y_p^2 \right)\]Ray fans:
\[\epsilon_y = -2 \frac{R}{r_p} W_{220} H^2 y_p\] \[\epsilon_x = -2 \frac{R}{r_p} W_{220} H^2 x_p\]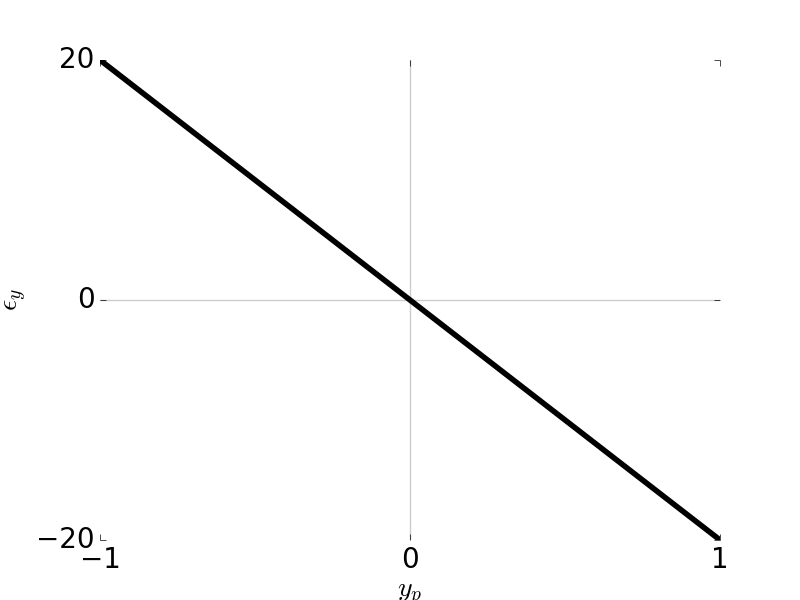
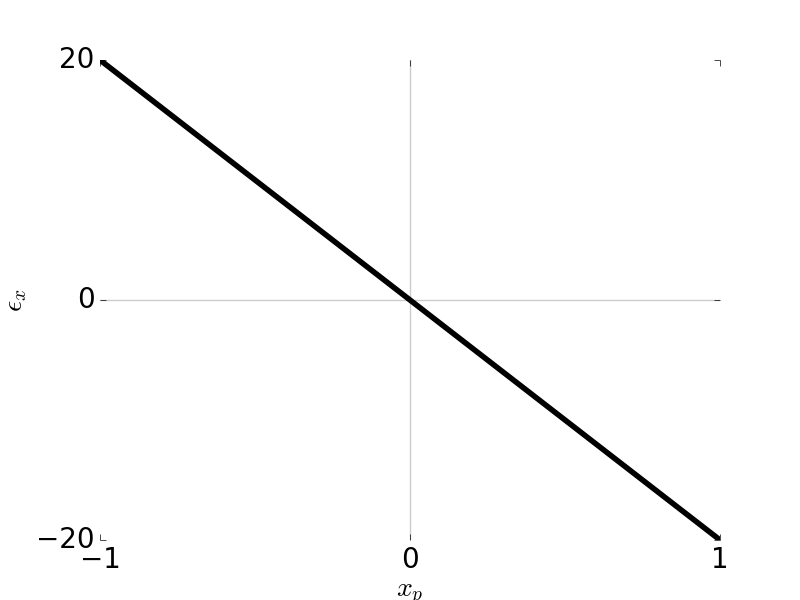 Tangential Ray and Sagittal Ray Fans: Field Curvature \(W_{220} = 1\), \( H \) = 1, \( F / \# \) = 5
Tangential Ray and Sagittal Ray Fans: Field Curvature \(W_{220} = 1\), \( H \) = 1, \( F / \# \) = 5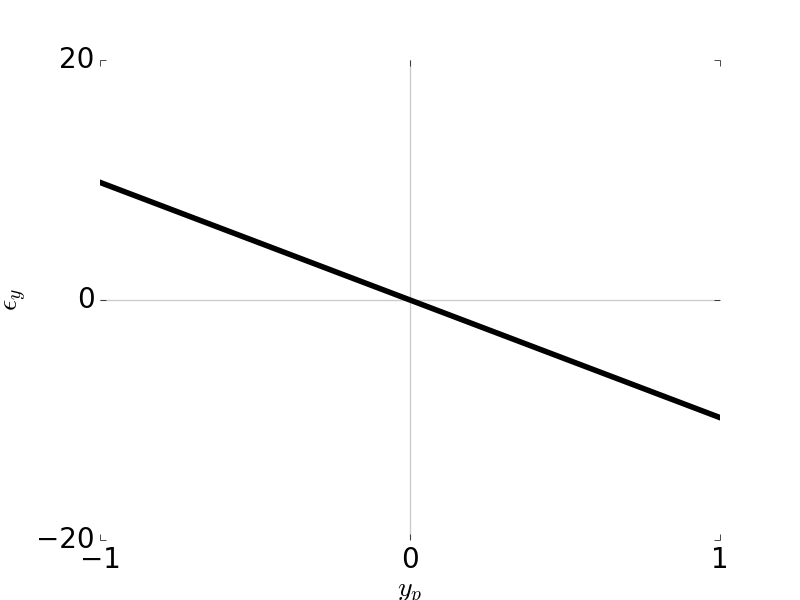
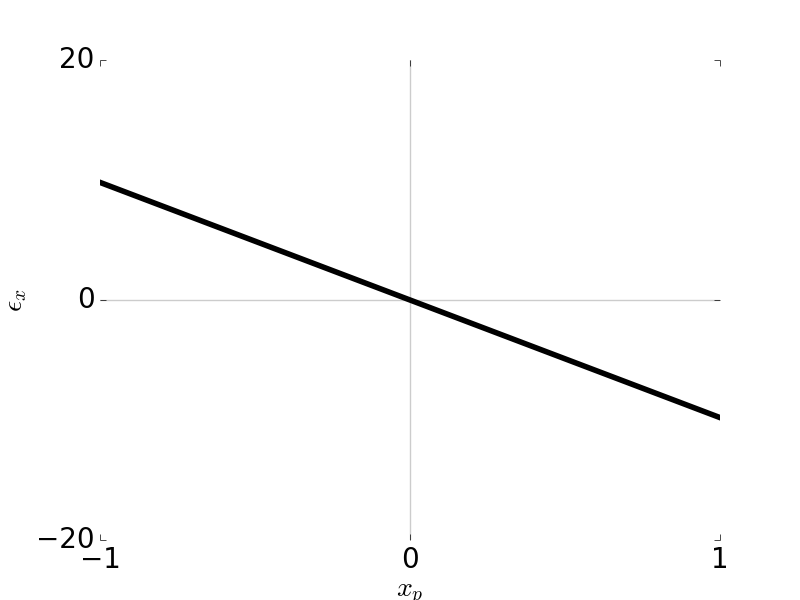 Tangential Ray and Sagittal Ray Fans: Coma \(W_{220} = 1\), \( H \) = 0.7, \( F / \# \) = 5
Tangential Ray and Sagittal Ray Fans: Coma \(W_{220} = 1\), \( H \) = 0.7, \( F / \# \) = 5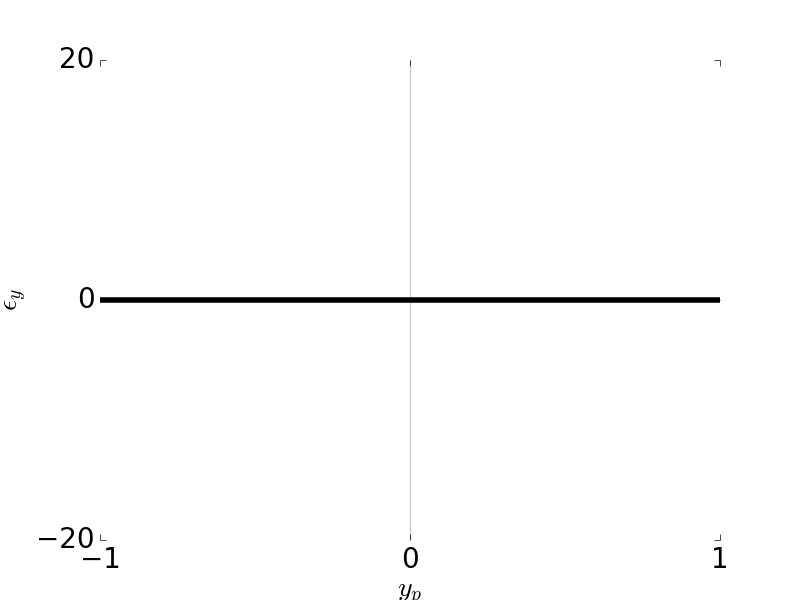
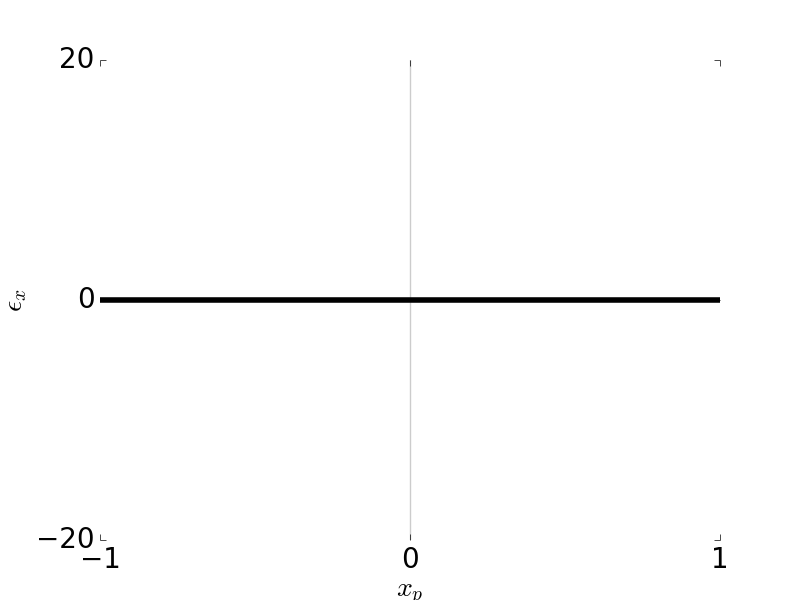 Tangential Ray and Sagittal Ray Fans: Field Curvature \(W_{220} = 1\), \( H \) = 0, \( F / \# \) = 5
Tangential Ray and Sagittal Ray Fans: Field Curvature \(W_{220} = 1\), \( H \) = 0, \( F / \# \) = 5
Distortion:
-
Occurs when image magnificantion varies with the image height \(H\).
-
Straight lines in the object appear as curved lines in the image.
-
Since points still map to points, there is no image blurring.
-
Barrel distortion results with the actual magnification is less than the paraxial magnification with increasing \(H\).
-
Pincushion distortion results when the actual magnification is larger than the paraxial magnification with increasing \(H\).
Wavefront aberration error:
\[W = W_{311} H^3 \rho \cos \theta = W_{311} H^3 y_p\]Ray fans:
\[\epsilon_y = -\frac{R}{r_p} W_{311} H^3\] \[\epsilon_x = 0\]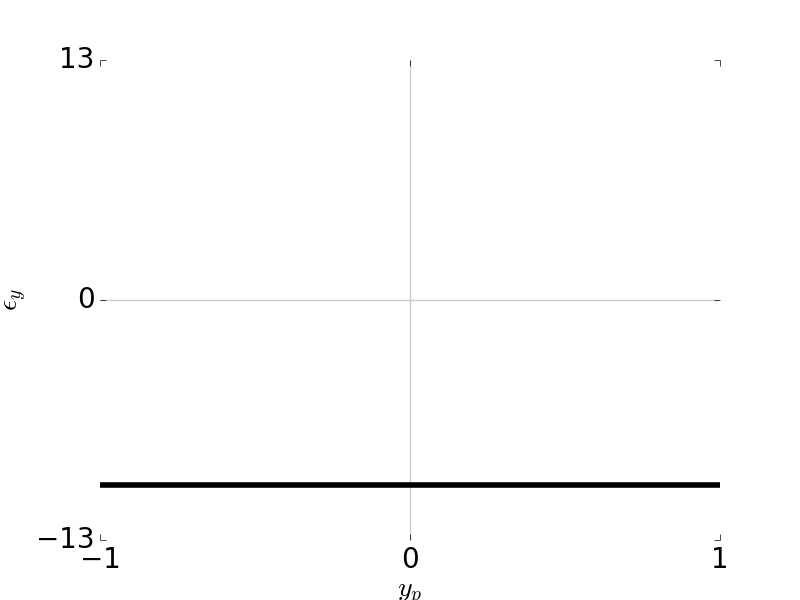
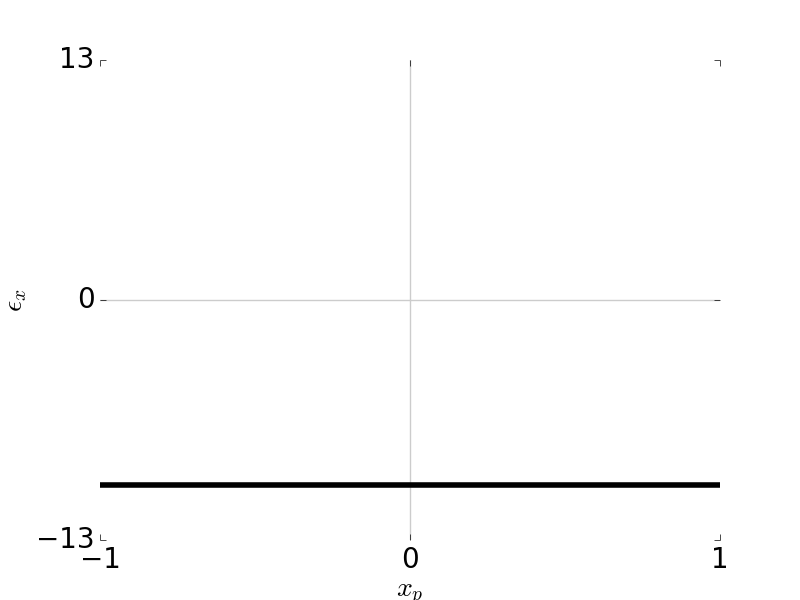 Tangential Ray and Sagittal Ray Fans: Distortion \(W_{311} = 1\), \( H \) = 1, \( F / \# \) = 5
Tangential Ray and Sagittal Ray Fans: Distortion \(W_{311} = 1\), \( H \) = 1, \( F / \# \) = 5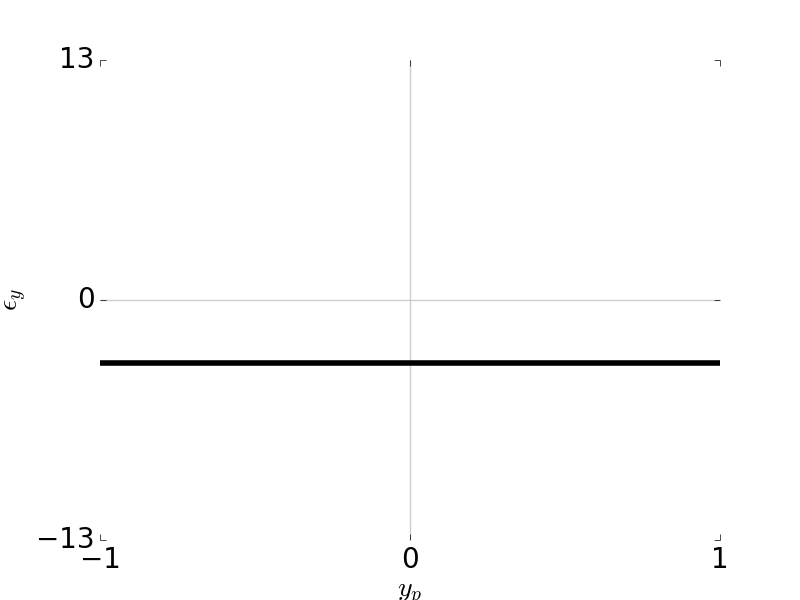
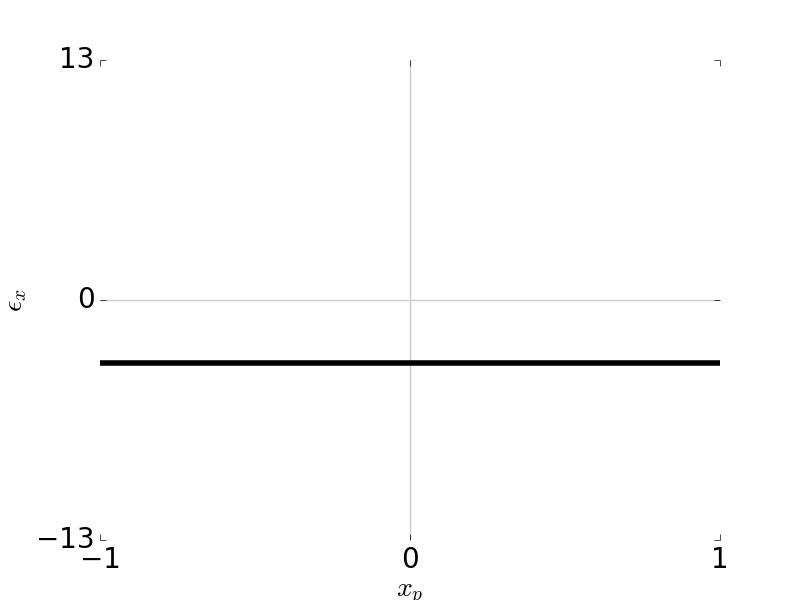 Tangential Ray and Sagittal Ray Fans: Distortion \(W_{311} = 1\), \( H \) = 0.7, \( F / \# \) = 5
Tangential Ray and Sagittal Ray Fans: Distortion \(W_{311} = 1\), \( H \) = 0.7, \( F / \# \) = 5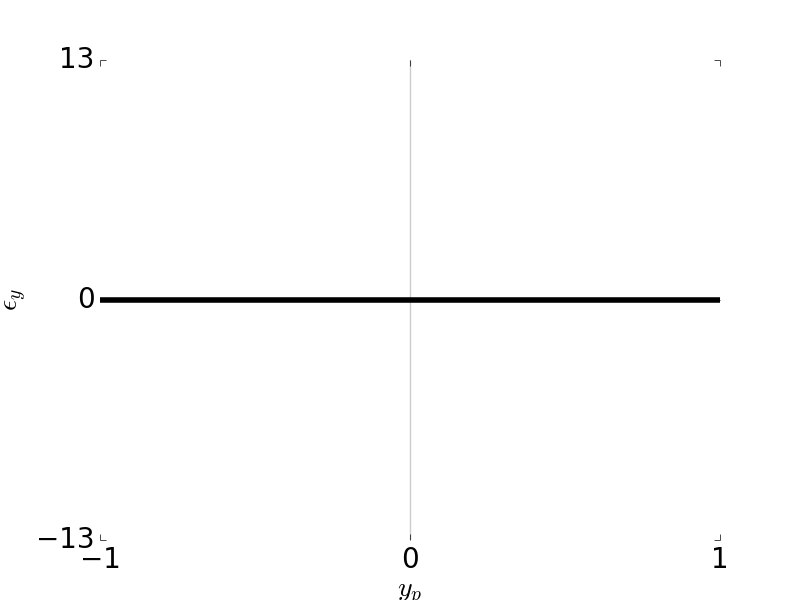
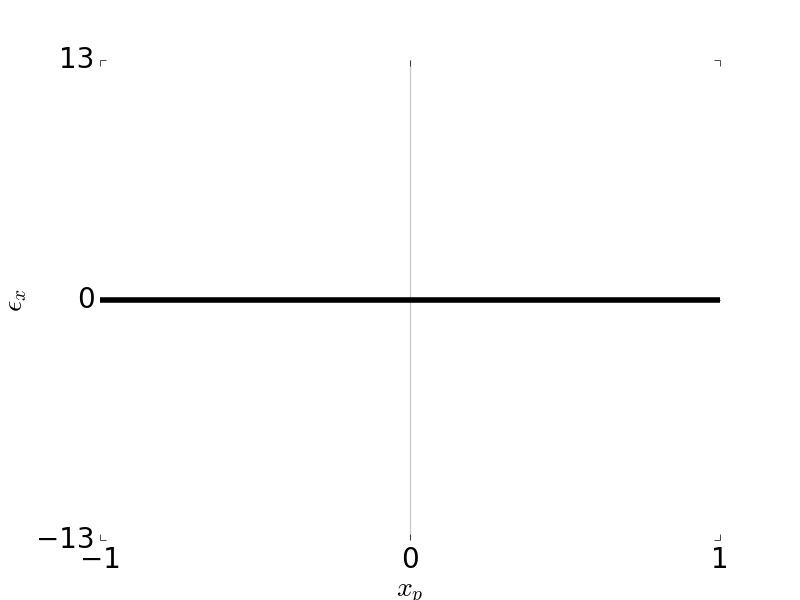 Tangential Ray and Sagittal Ray Fans: Distortion \(W_{311} = 1\), \( H \) = 0, \( F / \# \) = 5
Tangential Ray and Sagittal Ray Fans: Distortion \(W_{311} = 1\), \( H \) = 0, \( F / \# \) = 5
Combinations of Aberrations:
The ray fans encode the aberration in the dependnace of the ray errors on \(x_p\), \(y_p\), and \(H\).
| Aberration | Coefficient | $$ \epsilon_y \text{ vs. } y_p $$ | $$ \epsilon_x \text{ vs. } x_p $$ | $$H$$ |
| Wavefront tilt | $$W_{111}$$ | $$\text{constant}$$ | $$ 0 $$ | $$H$$ |
| Distortion | $$W_{311}$$ | $$\text{constant}$$ | $$ 0 $$ | $$H^3$$ |
| Defocus | $$\Delta W_{20}$$ | $$y_p$$ | $$x_p$$ | $$\text{none}$$ |
| Field Curvature | $$ W_{220}$$ | $$y_p$$ | $$x_p$$ | $$H^2$$ |
| Astigmatism | $$ W_{222}$$ | $$y_p$$ | $$0$$ | $$H^2$$ |
| Coma | $$ W_{131}$$ | $$y_p^2$$ | $$0$$ | $$H$$ |
| Spherical Aberration | $$ W_{040}$$ | $$y_p^3$$ | $$x_p^3$$ | $$\text{none}$$ |